In fluid dynamics, Airy wave theory (often referred to as linear wave theory) gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.^[1]

Airy wave theory is often applied in ocean engineering and coastal engineering for the modelling of random sea states – giving a description of the wave kinematics and dynamics of high-enough accuracy for many purposes.^[2][3] Further, several second-order nonlinear properties of surface gravity waves, and their propagation, can be estimated from its results.^[4] Airy wave theory is also a good approximation for tsunami waves in the ocean, before they steepen near the coast.

This linear theory is often used to get a quick and rough estimate of wave characteristics and their effects. This approximation is accurate for small ratios of the wave height to water depth (for waves in shallow water), and wave height to wavelength (for waves in deep water).

Description

Airy wave theory uses a potential flow (or velocity potential) approach to describe the motion of gravity waves on a fluid surface. The use of (inviscid and irrotational) potential flow in water waves is remarkably successful, given its failure to describe many other fluid flows where it is often essential to take viscosity, vorticity, turbulence or flow separation into account. This is due to the fact that for the oscillatory part of the fluid motion, wave-induced vorticity is restricted to some thin oscillatory Stokes boundary layers at the boundaries of the fluid domain.^[5]

Airy wave theory is often used in ocean engineering and coastal engineering. Especially for random waves, sometimes called wave turbulence, the evolution of the wave statistics – including the wave spectrum – is predicted well over not too long distances (in terms of wavelengths) and in not too shallow water. Diffraction is one of the wave effects which can be described with Airy wave theory. Further, by using the WKBJ approximation, wave shoaling and refraction can be predicted.^[2]

Earlier attempts to describe surface gravity waves using potential flow were made by, among others, Laplace, Poisson, Cauchy and Kelland. But Airy was the first to publish the correct derivation and formulation in 1841.^[1] Soon after, in 1847, the linear theory of Airy was extended by Stokes for non-linear wave motion – known as Stokes' wave theory – correct up to third order in the wave steepness.^[6] Even before Airy's linear theory, Gerstner derived a nonlinear trochoidal wave theory in 1802, which however is not irrotational.^[1]

Airy wave theory is a linear theory for the propagation of waves on the surface of a potential flow and above a horizontal bottom. The free surface elevation η(x,t) of one wave component is sinusoidal, as a function of horizontal position x and time t:

${\displaystyle \eta (x,t)=a\cos \left(kx-\omega t\right)}$

where

• a is the wave amplitude in metres,
• cos is the cosine function,
• k is the angular wavenumber in radians per metre, related to the wavelength λ by k = 2π/λ,
• ω is the angular frequency in radians per second, related to the period T and frequency f by ω = 2π/T = 2πf.

The waves propagate along the water surface with the phase speed c_p:

${\displaystyle c_{p}={\frac {\omega }{k}}={\frac {\lambda }{T}}.}$

The angular wavenumber k and frequency ω are not independent parameters (and thus also wavelength λ and period T are not independent), but are coupled. Surface gravity waves on a fluid are dispersive waves – exhibiting frequency dispersion – meaning that each wavenumber has its own frequency and phase speed.

Note that in engineering the wave height H – the difference in elevation between crest and trough – is often used:

${\displaystyle H=2a\quad {\text{and}}\quad a={\tfrac {1}{2}}H,}$

valid in the present case of linear periodic waves.

Underneath the surface, there is a fluid motion associated with the free surface motion. While the surface elevation shows a propagating wave, the fluid particles are in an orbital motion. Within the framework of Airy wave theory, the orbits are closed curves: circles in deep water and ellipses in finite depth—with the circles dying out before reaching the bottom of the fluid layer, and the ellipses becoming flatter near the bottom of the fluid layer. So while the wave propagates, the fluid particles just orbit (oscillate) around their average position. With the propagating wave motion, the fluid particles transfer energy in the wave propagation direction, without having a mean velocity. The diameter of the orbits reduces with depth below the free surface. In deep water, the orbit's diameter is reduced to 4% of its free-surface value at a depth of half a wavelength.

In a similar fashion, there is also a pressure oscillation underneath the free surface, with wave-induced pressure oscillations reducing with depth below the free surface – in the same way as for the orbital motion of fluid parcels.

Mathematical formulation of the wave motion

Flow problem formulation

The waves propagate in the horizontal direction, with coordinate x, and a fluid domain bound above by a free surface at z = η(x,t), with z the vertical coordinate (positive in the upward direction) and t being time.^[7] The level z = 0 corresponds with the mean surface elevation. The impermeable bed underneath the fluid layer is at z = −h. Further, the flow is assumed to be incompressible and irrotational – a good approximation of the flow in the fluid interior for waves on a liquid surface – and potential theory can be used to describe the flow. The velocity potential Φ(x, z, t) is related to the flow velocity components u_x and u_z in the horizontal (x) and vertical (z) directions by:

${\displaystyle u_{x}={\frac {\partial \Phi }{\partial x}}\quad {\text{and}}\quad u_{z}={\frac {\partial \Phi }{\partial z}}.}$

Then, due to the continuity equation for an incompressible flow, the potential Φ has to satisfy the Laplace equation:

$${\displaystyle {\frac {\partial ^{2}\Phi }{\partial x^{2}}}+{\frac {\partial ^{2}\Phi }{\partial z^{2}}}=0.}$$

(1)

Boundary conditions are needed at the bed and the free surface in order to close the system of equations. For their formulation within the framework of linear theory, it is necessary to specify what the base state (or zeroth-order solution) of the flow is. Here, we assume the base state is rest, implying the mean flow velocities are zero.

The bed being impermeable, leads to the kinematic bed boundary-condition:

$${\displaystyle {\frac {\partial \Phi }{\partial z}}=0\quad {\text{ at }}z=-h.}$$

(2)

In case of deep water – by which is meant infinite water depth, from a mathematical point of view – the flow velocities have to go to zero in the limit as the vertical coordinate goes to minus infinity: z → −∞.

At the free surface, for infinitesimal waves, the vertical motion of the flow has to be equal to the vertical velocity of the free surface. This leads to the kinematic free-surface boundary-condition:

$${\displaystyle {\frac {\partial \eta }{\partial t}}={\frac {\partial \Phi }{\partial z}}\quad {\text{ at }}z=\eta (x,t).}$$

(3)

If the free surface elevation η(x,t) was a known function, this would be enough to solve the flow problem. However, the surface elevation is an extra unknown, for which an additional boundary condition is needed. This is provided by Bernoulli's equation for an unsteady potential flow. The pressure above the free surface is assumed to be constant. This constant pressure is taken equal to zero, without loss of generality, since the level of such a constant pressure does not alter the flow. After linearisation, this gives the dynamic free-surface boundary condition:

$${\displaystyle {\frac {\partial \Phi }{\partial t}}+g\eta =0\quad {\text{ at }}z=\eta (x,t).}$$

(4)

Because this is a linear theory, in both free-surface boundary conditions – the kinematic and the dynamic one, equations (3) and (4) – the value of Φ and ∂Φ/∂z at the fixed mean level z = 0 is used.

Solution for a progressive monochromatic wave

For a propagating wave of a single frequency – a monochromatic wave – the surface elevation is of the form:^[7]

${\displaystyle \eta =a\cos(kx-\omega t).}$

The associated velocity potential, satisfying the Laplace equation (1) in the fluid interior, as well as the kinematic boundary conditions at the free surface (2), and bed (3), is:

${\displaystyle \Phi ={\frac {\omega }{k}}a{\frac {\cosh k(z+h)}{\sinh kh}}\sin(kx-\omega t),}$

with sinh and cosh the hyperbolic sine and hyperbolic cosine function, respectively. But η and Φ also have to satisfy the dynamic boundary condition, which results in non-trivial (non-zero) values for the wave amplitude a only if the linear dispersion relation is satisfied:

${\displaystyle \omega ^{2}=gk\tanh kh,}$

with tanh the hyperbolic tangent. So angular frequency ω and wavenumber k – or equivalently period T and wavelength λ – cannot be chosen independently, but are related. This means that wave propagation at a fluid surface is an eigenproblem. When ω and k satisfy the dispersion relation, the wave amplitude a can be chosen freely (but small enough for Airy wave theory to be a valid approximation).

Table of wave quantities

In the table below, several flow quantities and parameters according to Airy wave theory are given.^[7] The given quantities are for a bit more general situation as for the solution given above. Firstly, the waves may propagate in an arbitrary horizontal direction in the x = (x,y) plane. The wavenumber vector is k, and is perpendicular to the cams of the wave crests. Secondly, allowance is made for a mean flow velocity U, in the horizontal direction and uniform over (independent of) depth z. This introduces a Doppler shift in the dispersion relations. At an Earth-fixed location, the observed angular frequency (or absolute angular frequency) is ω. On the other hand, in a frame of reference moving with the mean velocity U (so the mean velocity as observed from this reference frame is zero), the angular frequency is different. It is called the intrinsic angular frequency (or relative angular frequency), denoted σ. So in pure wave motion, with U = 0, both frequencies ω and σ are equal. The wave number k (and wavelength λ) are independent of the frame of reference, and have no Doppler shift (for monochromatic waves).

The table only gives the oscillatory parts of flow quantities – velocities, particle excursions and pressure – and not their mean value or drift. The oscillatory particle excursions ξ_x and ξ_z are the time integrals of the oscillatory flow velocities u_x and u_z respectively.

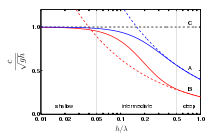
Water depth is classified into three regimes:^[8]

• deep water – for a water depth larger than half the wavelength, h > 1/2λ, the phase speed of the waves is hardly influenced by depth (this is the case for most wind waves on the sea and ocean surface),^[9]
• shallow water – for a water depth smaller than 5% of the wavelength, h < 1/20λ, the phase speed of the waves is only dependent on water depth, and no longer a function of period or wavelength;^[10] and
• intermediate depth – all other cases, 1/20λ < h < 1/2λ, where both water depth and period (or wavelength) have a significant influence on the solution of Airy wave theory.

In the limiting cases of deep and shallow water, simplifying approximations to the solution can be made. While for intermediate depth, the full formulations have to be used.

Properties of gravity waves on the surface of deep water, shallow water and at intermediate depth, according to Airy wave theory[7]
quantity	symbol	units	deep water (h > 1/2λ)	shallow water (h < 1/20λ)	intermediate depth (all λ and h)
surface elevation	${\displaystyle \eta (\mathbf {x} ,t)}$	m	${\displaystyle a\cos \theta (\mathbf {x} ,t)}$
wave phase	${\displaystyle \theta (\mathbf {x} ,t)}$	rad	${\displaystyle \mathbf{k}\cdot <!--\; \cdot \; -->}$Zdroj:https://en.wikipedia.org?pojem=Airy_wave_theory >Text je dostupný pod licencí Creative Commons Uveďte autora – Zachovejte licenci, případně za dalších podmínek. Podrobnosti naleznete na stránce Podmínky užití. Zdroj: Wikipedia.org - čítajte viac o Airy wave theory Navigace: Módní doplňky > Šperkařství Šperky Chytré hodinky Galanterie Hodinářské firmy Hodinky Hodiny Módní doplňky Minerály Pokrývky hlavy Sklářství Zlatníci Zlatnictví Příbuzné výrazy : Řetízek (ozdoba) Šátek Beadweaving Bižuterie Bolo Dřevěný motýlek Deštník Digitálky Fiží Galanterie Hodinky Kšandy Kapesník Korálek Kravata Lanyard Modista Motýlek (oděvní doplněk) Odznak Pléd Placka (odznak) Rukávník Spona na kravatu Sponka do vlasů Tabulky (kolárek) Vějíř Text je dostupný za podmienok Creative Commons Attribution/Share-Alike License 3.0 Unported; prípadne za ďalších podmienok. Podrobnejšie informácie nájdete na stránke Podmienky použitia. Copyright.sk © 2024