In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.

For curves, the canonical example is that of a circle, which has a curvature equal to the reciprocal of its radius. Smaller circles bend more sharply, and hence have higher curvature. The curvature at a point of a differentiable curve is the curvature of its osculating circle, that is the circle that best approximates the curve near this point. The curvature of a straight line is zero. In contrast to the tangent, which is a vector quantity, the curvature at a point is typically a scalar quantity, that is, it is expressed by a single real number.

For surfaces (and, more generally for higher-dimensional manifolds), that are embedded in a Euclidean space, the concept of curvature is more complex, as it depends on the choice of a direction on the surface or manifold. This leads to the concepts of maximal curvature, minimal curvature, and mean curvature.

For Riemannian manifolds (of dimension at least two) that are not necessarily embedded in a Euclidean space, one can define the curvature intrinsically, that is without referring to an external space. See Curvature of Riemannian manifolds for the definition, which is done in terms of lengths of curves traced on the manifold, and expressed, using linear algebra, by the Riemann curvature tensor.

History

This section needs expansion. You can help by adding to it. (October 2019)

In Tractatus de configurationibus qualitatum et motuum,^[1] the 14th-century philosopher and mathematician Nicole Oresme introduces the concept of curvature as a measure of departure from straightness; for circles he has the curvature as being inversely proportional to the radius; and he attempts to extend this idea to other curves as a continuously varying magnitude. ^[2]

The curvature of a differentiable curve was originally defined through osculating circles. In this setting, Augustin-Louis Cauchy showed that the center of curvature is the intersection point of two infinitely close normal lines to the curve.^[3]

Plane curves

Intuitively, the curvature describes for any part of a curve how much the curve direction changes over a small distance travelled (e.g. angle in rad/m), so it is a measure of the instantaneous rate of change of direction of a point that moves on the curve: the larger the curvature, the larger this rate of change. In other words, the curvature measures how fast the unit tangent vector to the curve rotates^[4] (fast in terms of curve position). In fact, it can be proved that this instantaneous rate of change is exactly the curvature. More precisely, suppose that the point is moving on the curve at a constant speed of one unit, that is, the position of the point P(s) is a function of the parameter s, which may be thought as the time or as the arc length from a given origin. Let T(s) be a unit tangent vector of the curve at P(s), which is also the derivative of P(s) with respect to s. Then, the derivative of T(s) with respect to s is a vector that is normal to the curve and whose length is the curvature.

For being meaningful, the definition of the curvature and its different characterizations require that the curve is continuously differentiable near P, for having a tangent that varies continuously; it requires also that the curve is twice differentiable at P, for insuring the existence of the involved limits, and of the derivative of T(s).

The characterization of the curvature in terms of the derivative of the unit tangent vector is probably less intuitive than the definition in terms of the osculating circle, but formulas for computing the curvature are easier to deduce. Therefore, and also because of its use in kinematics, this characterization is often given as a definition of the curvature.

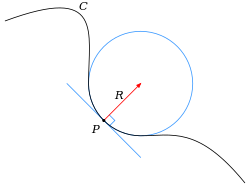
Osculating circle

Historically, the curvature of a differentiable curve was defined through the osculating circle, which is the circle that best approximates the curve at a point. More precisely, given a point P on a curve, every other point Q of the curve defines a circle (or sometimes a line) passing through Q and tangent to the curve at P. The osculating circle is the limit, if it exists, of this circle when Q tends to P. Then the center and the radius of curvature of the curve at P are the center and the radius of the osculating circle. The curvature is the reciprocal of radius of curvature. That is, the curvature is

${\displaystyle \kappa ={\frac {1}{R}},}$

where R is the radius of curvature^[5] (the whole circle has this curvature, it can be read as turn 2π over the length 2πR).

This definition is difficult to manipulate and to express in formulas. Therefore, other equivalent definitions have been introduced.

In terms of arc-length parametrization

Every differentiable curve can be parametrized with respect to arc length.^[6] In the case of a plane curve, this means the existence of a parametrization γ(s) = (x(s), y(s)), where x and y are real-valued differentiable functions whose derivatives satisfy

${\displaystyle \|{\boldsymbol {\gamma }}'\|={\sqrt {x'(s)^{2}+y'(s)^{2}}}=1.}$

This means that the tangent vector

${\displaystyle \mathbf {T} (s)={\bigl (}x'(s),y'(s){\bigr )}}$

has a norm equal to one and is thus a unit tangent vector.

If the curve is twice differentiable, that is, if the second derivatives of x and y exist, then the derivative of T(s) exists. This vector is normal to the curve, its norm is the curvature κ(s), and it is oriented toward the center of curvature. That is,

${\displaystyle {\begin{aligned}&\mathbf {T} (s)={\boldsymbol {\gamma }}'(s),\\&\mathbf {T} ^{2}(s)=1\ {\text{(constant)}}\implies \mathbf {T} '(s)\cdot \mathbf {T} (s)=0\\&\kappa (s)=\|\mathbf {T} '(s)\|=\|{\boldsymbol {\gamma }}''(s)\|={\sqrt {x''(s)^{2}+y''(s)^{2}}}\\\end{aligned}}}$

Moreover, as the radius of curvature is

${\displaystyle R(s)={\frac {1}{\kappa (s)}},}$

and the center of curvature is on the normal to the curve, the center of curvature is the point

${\displaystyle \mathbf {C} (s)={\boldsymbol {\gamma }}(s)+{\frac {1}{\kappa (s)^{2}}}\mathbf {T} '(s).}$

If N(s) is the unit normal vector obtained from T(s) by a counterclockwise rotation of π/2, then

${\displaystyle \mathbf {T} '(s)=k(s)\mathbf {N} (s),}$

with k(s) = ± κ(s). The real number k(s) is called the oriented curvature or signed curvature. It depends on both the orientation of the plane (definition of counterclockwise), and the orientation of the curve provided by the parametrization. In fact, the change of variable s → –s provides another arc-length parametrization, and changes the sign of k(s).

In terms of a general parametrization

Let γ(t) = (x(t), y(t)) be a proper parametric representation of a twice differentiable plane curve. Here proper means that on the domain of definition of the parametrization, the derivative dγ/dt is defined, differentiable and nowhere equal to the zero vector.

With such a parametrization, the signed curvature is

${\displaystyle k={\frac {x'y''-y'x''}{\left({x'}^{2}+{y'}^{2}\right)^{\frac {3}{2}}}},}$

where primes refer to derivatives with respect to t. The curvature κ is thus

${\displaystyle \kappa ={\frac {|x'y''-y'x''|}{\left({x'}^{2}+{y'}^{2}\right)^{\frac {3}{2}}}}.}$

These can be expressed in a coordinate-free way as

${\displaystyle k={\frac {\det({\boldsymbol {\gamma }}',{\boldsymbol {\gamma }}'')}{\|{\boldsymbol {\gamma }}'\|^{3}}},\qquad \kappa ={\frac {|\det({\boldsymbol {\gamma }}',{\boldsymbol {\gamma }}'')|}{\|{\boldsymbol {\gamma }}'\|^{3}}}.}$

These formulas can be derived from the special case of arc-length parametrization in the following way. The above condition on the parametrisation imply that the arc length s is a differentiable monotonic function of the parameter t, and conversely that t is a monotonic function of s. Moreover, by changing, if needed, s to –s, one may suppose that these functions are increasing and have a positive derivative. Using notation of the preceding section and the chain rule, one has

${\displaystyle {\frac {d{\boldsymbol {\gamma }}}{dt}}={\frac {ds}{dt}}\mathbf {T} ,}$

and thus, by taking the norm of both sides

${\displaystyle {\frac {dt}{ds}}={\frac {1}{\|{\boldsymbol {\gamma }}'\|}},}$

where the prime denotes differentiation with respect to t.

The curvature is the norm of the derivative of T with respect to s. By using the above formula and the chain rule this derivative and its norm can be expressed in terms of γ′ and γ″ only, with the arc-length parameter s completely eliminated, giving the above formulas for the curvature.

Graph of a function

The graph of a function y = f(x), is a special case of a parametrized curve, of the form

${\displaystyle {\begin{aligned}x&=t\\y&=f(t).\end{aligned}}}$

As the first and second derivatives of x are 1 and 0, previous formulas simplify to

${\displaystyle \kappa ={\frac {|y''|}{\left(1+{y'}^{2}\right)^{\frac {3}{2}}}},}$

for the curvature, and to

${\displaystyle k={\frac {y''}{\left(1+{y'}^{2}\right)^{\frac {3}{2}}}},}$

for the signed curvature.

In the general case of a curve, the sign of the signed curvature is somewhat arbitrary, as it depends on the orientation of the curve. In the case of the graph of a function, there is a natural orientation by increasing values of x. This makes significant the sign of the signed curvature.

The sign of the signed curvature is the same as the sign of the second derivative of f. If it is positive then the graph has an upward concavity, and, if it is negative the graph has a downward concavity. It is zero, then one has an inflection point or an undulation point.

When the slope of the graph (that is the derivative of the function) is small, the signed curvature is well approximated by the second derivative. More precisely, using big O notation, one has

${\displaystyle k(x)=y''\left(1+O\left({y'}^{2}\right)\right).}$

It is common in physics and engineering to approximate the curvature with the second derivative, for example, in beam theory or for deriving wave equation of a tense string, and other applications where small slopes are involved. This often allows systems that are otherwise nonlinear to be considered as linear.

Polar coordinates

If a curve is defined in polar coordinates by the radius expressed as a function of the polar angle, that is r is a function of θ, then its curvature is

${\displaystyle \kappa (\theta )={\frac {\left|r^{2}+2{r'}^{2}-r\,r''\right|}{\left(r^{2}+{r'}^{2}\right)^{\frac {3}{2}}}}}$

where the prime refers to differentiation with respect to θ.

This results from the formula for general parametrizations, by considering the parametrization

${\displaystyle {\begin{aligned}x&=r(\theta )\cos \theta \\y&=r(\theta )\sin \theta \end{aligned}}}$

Implicit curve

For a curve defined by an implicit equation F(x, y) = 0 with partial derivatives denoted F_x, F_y, F_xx, F_xy, F_yy, the curvature is given by^[7]

${\displaystyle \kappa ={\frac {\left|F_{y}^{2}F_{xx}-2F_{x}F_{y}F_{xy}+F_{x}^{2}F_{yy}\right|}{\left(F_{x}^{2}+F_{y}^{2}\right)^{\frac {3}{2}}}}.}$

The signed curvature is not defined, as it depends on an orientation of the curve that is not provided by the implicit equation. Also, changing F into –F does not change the curve, but changes the sign of the numerator if the absolute value is omitted in the preceding formula.

A point of the curve where F_x = F_y = 0 is a singular point, which means that the curve is not differentiable at this point, and thus that the curvature is not defined (most often, the point is either a crossing point or a cusp).

Above formula for the curvature can be derived from the expression of the curvature of the graph of a function by using the implicit function theorem and the fact that, on such a curve, one has

${\displaystyle {\frac {dy}{dx}}=-{\frac {F_{x}}{F_{y}}}.}$

Examples

It can be useful to verify on simple examples that the different formulas given in the preceding sections give the same result.

Circle

A common parametrization of a circle of radius r is γ(t) = (r cos t, r sin t). The formula for the curvature gives

${\displaystyle k(t)=\frac{r^2{\sin }^2<!--\; \; -->t+r^2{\cos }^2<!--\; \; -->t}{(r^2{\cos }^2<!--\; \; -->t+r^2}}$Zdroj:https://en.wikipedia.org?pojem=Curvature
>Text je dostupný pod licencí Creative Commons Uveďte autora – Zachovejte licenci, případně za dalších podmínek. Podrobnosti naleznete na stránce Podmínky užití.

---