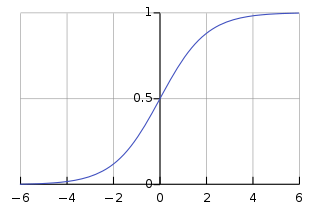
A sigmoid function is any mathematical function whose graph has a characteristic S-shaped curve or sigmoid curve.

A common example of a sigmoid function is the logistic function shown in the first figure and defined by the formula:^[1]

${\displaystyle \sigma (x)={\frac {1}{1+e^{-x}}}={\frac {e^{x}}{1+e^{x}}}=1-\sigma (-x).}$

Other standard sigmoid functions are given in the Examples section. In some fields, most notably in the context of artificial neural networks, the term "sigmoid function" is used as an alias for the logistic function.

Special cases of the sigmoid function include the Gompertz curve (used in modeling systems that saturate at large values of x) and the ogee curve (used in the spillway of some dams). Sigmoid functions have domain of all real numbers, with return (response) value commonly monotonically increasing but could be decreasing. Sigmoid functions most often show a return value (y axis) in the range 0 to 1. Another commonly used range is from −1 to 1.

A wide variety of sigmoid functions including the logistic and hyperbolic tangent functions have been used as the activation function of artificial neurons. Sigmoid curves are also common in statistics as cumulative distribution functions (which go from 0 to 1), such as the integrals of the logistic density, the normal density, and Student's t probability density functions. The logistic sigmoid function is invertible, and its inverse is the logit function.

Definition

A sigmoid function is a bounded, differentiable, real function that is defined for all real input values and has a non-negative derivative at each point^{[1] [2]} and exactly one inflection point.

Properties

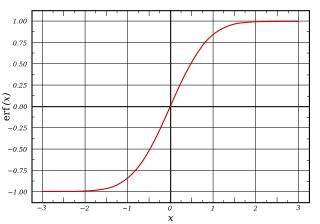
In general, a sigmoid function is monotonic, and has a first derivative which is bell shaped. Conversely, the integral of any continuous, non-negative, bell-shaped function (with one local maximum and no local minimum, unless degenerate) will be sigmoidal. Thus the cumulative distribution functions for many common probability distributions are sigmoidal. One such example is the error function, which is related to the cumulative distribution function of a normal distribution; another is the arctan function, which is related to the cumulative distribution function of a Cauchy distribution.

A sigmoid function is constrained by a pair of horizontal asymptotes as ${\displaystyle x\rightarrow \pm \infty }$.

A sigmoid function is convex for values less than a particular point, and it is concave for values greater than that point: in many of the examples here, that point is 0.

Examples

• Logistic function
  $${\displaystyle f(x)={\frac {1}{1+e^{-x}}}}$$

  
• Hyperbolic tangent (shifted and scaled version of the logistic function, above)
  $${\displaystyle f(x)=\tanh x={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}$$

  
• Arctangent function
  $${\displaystyle f(x)=\arctan x}$$

  
• Gudermannian function
  $${\displaystyle f(x)=\operatorname {gd} (x)=\int _{0}^{x}{\frac {dt}{\cosh t}}=2\arctan \left(\tanh \left({\frac {x}{2}}\right)\right)}$$

  
• Error function
  $${\displaystyle f(x)=\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt}$$

  
• Generalised logistic function
  $${\displaystyle f(x)=\left(1+e^{-x}\right)^{-\alpha },\quad \alpha >0}$$

  
• Smoothstep function
  $${\displaystyle f(x)={\begin{cases}{\displaystyle \left(\int _{0}^{1}\left(1-u^{2}\right)^{N}du\right)^{-1}\int _{0}^{x}\left(1-u^{2}\right)^{N}\ du},&|x|\leq 1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\quad N\in \mathbb {Z} \geq 1}$$

  
• Some algebraic functions, for example
  $${\displaystyle f(x)={\frac {x}{\sqrt {1+x^{2}}}}}$$

  
• and in a more general form^[3]
  $${\displaystyle f(x)={\frac {x}{\left(1+|x|^{k}\right)^{1/k}}}}$$

  
• Up to shifts and scaling, many sigmoids are special cases of
  $${\displaystyle f(x)=\varphi (\varphi (x,\beta ),\alpha ),}$$

  
  where
  $${\displaystyle \varphi (x,\lambda )={\begin{cases}(1-\lambda x)^{1/\lambda }&\lambda \neq 0\\e^{-x}&\lambda =0\\\end{cases}}}$$

  
  is the inverse of the negative Box–Cox transformation, and ${\displaystyle \alpha <1}$ and ${\displaystyle \beta <1}$ are shape parameters.^[4]
• Smooth Interpolation^[5] normalized to (-1,1) and ${\displaystyle n}$ is the slope at zero: