Cutaway of a nautilus shell showing the chambers arranged in an approximately logarithmic spiral

In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point.^[1][2][3][4]

Helices

An Archimedean spiral (black), a helix (green), and a conic spiral (red)

Two major definitions of "spiral" in the American Heritage Dictionary are:^[5]

1. a curve on a plane that winds around a fixed center point at a continuously increasing or decreasing distance from the point.
2. a three-dimensional curve that turns around an axis at a constant or continuously varying distance while moving parallel to the axis; a helix.

The first definition describes a planar curve, that extends in both of the perpendicular directions within its plane; the groove on one side of a record closely approximates a plane spiral (and it is by the finite width and depth of the groove, but not by the wider spacing between than within tracks, that it falls short of being a perfect example); note that successive loops differ in diameter. In another example, the "center lines" of the arms of a spiral galaxy trace logarithmic spirals.

The second definition includes two kinds of 3-dimensional relatives of spirals:

1. a conical or volute spring (including the spring used to hold and make contact with the negative terminals of AA or AAA batteries in a battery box), and the vortex that is created when water is draining in a sink is often described as a spiral, or as a conical helix.
2. quite explicitly, definition 2 also includes a cylindrical coil spring and a strand of DNA, both of which are quite helical, so that "helix" is a more useful description than "spiral" for each of them; in general, "spiral" is seldom applied if successive "loops" of a curve have the same diameter.^[5]

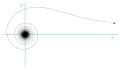
In the side picture, the black curve at the bottom is an Archimedean spiral, while the green curve is a helix. The curve shown in red is a conic helix.

Two-dimensional

A two-dimensional, or plane, spiral may be described most easily using polar coordinates, where the radius ${\displaystyle r}$ is a monotonic continuous function of angle ${\displaystyle \varphi }$:

• ${\displaystyle r=r(\varphi )\;.}$

The circle would be regarded as a degenerate case (the function not being strictly monotonic, but rather constant).

In ${\displaystyle x}$-${\displaystyle y}$-coordinates the curve has the parametric representation:

• ${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi \;.}$

Examples

Some of the most important sorts of two-dimensional spirals include:

• The Archimedean spiral: ${\displaystyle r=a\varphi }$
• The hyperbolic spiral: ${\displaystyle r=a/\varphi }$
• Fermat's spiral: ${\displaystyle r=a\varphi ^{1/2}}$
• The lituus: ${\displaystyle r=a\varphi ^{-1/2}}$
• The logarithmic spiral: ${\displaystyle r=ae^{k\varphi }}$
• The Cornu spiral or clothoid
• The Fibonacci spiral and golden spiral
• The Spiral of Theodorus: an approximation of the Archimedean spiral composed of contiguous right triangles
• The involute of a circle, used twice on each tooth of almost every modern gear

• 

  Archimedean spiral

• 

  hyperbolic spiral

• 

  Fermat's spiral

• 

  lituus

• 

  logarithmic spiral

• 

  Cornu spiral

• 

  spiral of Theodorus

• 

  Fibonacci Spiral (golden spiral)

• 

  The involute of a circle (black) is not identical to the Archimedean spiral (red).

Hyperbolic spiral as central projection of a helix

An Archimedean spiral is, for example, generated while coiling a carpet.^[6]

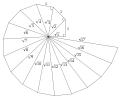
A hyperbolic spiral appears as image of a helix with a special central projection (see diagram). A hyperbolic spiral is some times called reciproke spiral, because it is the image of an Archimedean spiral with a circle-inversion (see below).^[7]

The name logarithmic spiral is due to the equation ${\displaystyle \varphi ={\tfrac {1}{k}}\cdot \ln {\tfrac {r}{a}}}$. Approximations of this are found in nature.

Spirals which do not fit into this scheme of the first 5 examples:

A Cornu spiral has two asymptotic points.
The spiral of Theodorus is a polygon.
The Fibonacci Spiral consists of a sequence of circle arcs.
The involute of a circle looks like an Archimedean, but is not: see Involute#Examples.

Geometric properties

The following considerations are dealing with spirals, which can be described by a polar equation ${\displaystyle r=r(\varphi )}$, especially for the cases ${\displaystyle r(\varphi )=a\varphi ^{n}}$ (Archimedean, hyperbolic, Fermat's, lituus spirals) and the logarithmic spiral ${\displaystyle r=ae^{k\varphi }}$.

Definition of sector (light blue) and polar slope angle ${\displaystyle \alpha }$

Polar slope angle

The angle ${\displaystyle \alpha }$ between the spiral tangent and the corresponding polar circle (see diagram) is called angle of the polar slope and ${\displaystyle \tan \alpha }$ the polar slope.

From vector calculus in polar coordinates one gets the formula

${\displaystyle \tan \alpha ={\frac {r'}{r}}\ .}$

Hence the slope of the spiral ${\displaystyle \;r=a\varphi ^{n}\;}$ is

• ${\displaystyle \tan \alpha ={\frac {n}{\varphi }}\ .}$

In case of an Archimedean spiral (${\displaystyle n=1}$) the polar slope is ${\displaystyle \;\tan \alpha ={\tfrac {1}{\varphi }}\ .}$

The logarithmic spiral is a special case, because of ${\displaystyle \ \tan \alpha =k\ }$ constant !

curvature

The curvature ${\displaystyle \kappa }$ of a curve with polar equation ${\displaystyle r=r(\varphi )}$ is

${\displaystyle \kappa ={\frac {r^{2}+2(r')^{2}-r\;r''}{(r^{2}+(r')^{2})^{3/2}}}\ .}$

For a spiral with ${\displaystyle r=a\varphi ^{n}}$ one gets

• ${\displaystyle \kappa =\dotsb ={\frac {1}{a\varphi ^{n-1}}}{\frac {\varphi ^{2}+n^{2}+n}{(\varphi ^{2}+n^{2})^{3/2}}}\ .}$

In case of ${\displaystyle n=1}$ (Archimedean spiral) ${\displaystyle \kappa ={\tfrac {\varphi ^{2}+2}{a(\varphi ^{2}+1)^{3/2}}}}$.
Only for ${\displaystyle -1<n<0}$ the spiral has an inflection point.

The curvature of a logarithmic spiral ${\displaystyle \;r=ae^{k\varphi }\;}$ is ${\displaystyle \;\kappa ={\tfrac {1}{r{\sqrt {1+k^{2}}}}}\;.}$

Sector area

The area of a sector of a curve (see diagram) with polar equation ${\displaystyle r=r(\varphi )}$ is

${\displaystyle A={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\;d\varphi \ .}$

For a spiral with equation ${\displaystyle r=a\varphi ^{n}\;}$ one gets

• ${\displaystyle A={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}a^{2}\varphi ^{2n}\;d\varphi ={\frac {a^{2}}{2(2n+1)}}{\big (}\varphi _{2}^{2n+1}-\varphi _{1}^{2n+1}{\big )}\ ,\quad {\text{if}}\quad n\neq -{\frac {1}{2}},}$

${\displaystyle A={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}{\frac {a^{2}}{\varphi }}\;d\varphi ={\frac {a^{2}}{2}}(\ln \varphi _{2}-\ln \varphi _{1})\ ,\quad {\text{if}}\quad n=-{\frac {1}{2}}\ .}$

The formula for a logarithmic spiral ${\displaystyle \;r=ae^{k\varphi }\;}$ is ${\displaystyle \ A={\tfrac {r(\varphi _{2})^{2}-r(\varphi _{1})^{2})}{4k}}\ .}$

Arc length

The length of an arc of a curve with polar equation ${\displaystyle r=r(\varphi )}$ is

${\displaystyle L=\underset{{\mathrm{\phi <!--\; \phi \; -->}}_1}{\overset{{\mathrm{\phi <!--\; \phi \; -->}}_2}{\int <!--\; \int \; -->}}\sqrt{{\left(r^{\mathrm{\prime <!--\; \prime \; -->}}(\mathrm{\phi <!--\; \phi \; -->})\right)}^2+r^2(\mathrm{\phi <!--\; \phi \; -->})}}$Zdroj:https://en.wikipedia.org?pojem=Spirals
>Text je dostupný pod licencí Creative Commons Uveďte autora – Zachovejte licenci, případně za dalších podmínek. Podrobnosti naleznete na stránce Podmínky užití.

---