In fluid dynamics, drag (sometimes called fluid resistance) is a force acting opposite to the relative motion of any object moving with respect to a surrounding fluid.^[1] This can exist between two fluid layers (or surfaces) or between a fluid and a solid surface.

Unlike other resistive forces, such as dry friction, which are nearly independent of velocity, the drag force depends on velocity.^[2][3] Drag force is proportional to the velocity for low-speed flow and the squared velocity for high speed flow, where the distinction between low and high speed is measured by the Reynolds number.

Drag forces always tend to decrease fluid velocity relative to the solid object in the fluid's path.

Examples

Examples of drag include the component of the net aerodynamic or hydrodynamic force acting opposite to the direction of movement of a solid object such as cars (automobile drag coefficient), aircraft^[3] and boat hulls; or acting in the same geographical direction of motion as the solid, as for sails attached to a down wind sail boat, or in intermediate directions on a sail depending on points of sail.^[4][5][6] In the case of viscous drag of fluid in a pipe, drag force on the immobile pipe decreases fluid velocity relative to the pipe.^[7][8]

In the physics of sports, the drag force is necessary to explain the motion of balls, javelins, arrows and frisbees and the performance of runners and swimmers.^[9]

Types

Shape and flow	Form Drag	Skin friction
	≈0%	≈100%
	≈10%	≈90%
	≈90%	≈10%
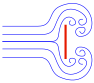
	≈100%	≈0%

Types of drag are generally divided into the following categories:

• form drag or pressure drag due to the size and shape of a body
• skin friction drag or viscous drag due to the friction between the fluid and a surface which may be the outside of an object or inside such as the bore of a pipe

The effect of streamlining on the relative proportions of skin friction and form drag is shown for two different body sections, an airfoil, which is a streamlined body, and a cylinder, which is a bluff body. Also shown is a flat plate illustrating the effect that orientation has on the relative proportions of skin friction and pressure difference between front and back. A body is known as bluff (or blunt) if the source of drag is dominated by pressure forces and streamlined if the drag is dominated by viscous forces. Road vehicles are bluff bodies.^[10] For aircraft, pressure and friction drag are included in the definition of parasitic drag. Parasite drag is often expressed in terms of a hypothetical (in so far as there is no edge spillage drag^[11]) "equivalent parasite drag area" which is the area of a flat plate perpendicular to the flow. It is used for comparing the drag of different aircraft. For example, the Douglas DC-3 has an equivalent parasite area of 23.7 sq ft and the McDonnell Douglas DC-9, with 30 years of advancement in aircraft design, an area of 20.6 sq ft although it carried five times as many passengers.^[12]

• lift-induced drag appears with wings or a lifting body in aviation and with semi-planing or planing hulls for watercraft
• wave drag (aerodynamics) is caused by the presence of shockwaves and first appears at subsonic aircraft speeds when local flow velocities become supersonic. The wave drag of the supersonic Concorde prototype aircraft was reduced at Mach 2 by 1.8% by applying the area rule which extended the rear fuselage 3.73m on the production aircraft.^[13]
• wave resistance (ship hydrodynamics) or wave drag occurs when a solid object is moving along a fluid boundary and making surface waves
• boat-tail drag on an aircraft is caused by the angle with which the rear fuselage, or engine nacelle, narrows to the engine exhaust diameter.^[14]

• 

  Concorde with 'high' wave drag tail

• 

  Concorde with 'low' wave drag tail (N.B. rear fuselage spike)

• 

  Hawk aircraft showing base area above circular engine exhaust

The drag equation

Drag depends on the properties of the fluid and on the size, shape, and speed of the object. One way to express this is by means of the drag equation:

where

• ${\displaystyle F_{D}}$ is the drag force,
• ${\displaystyle \rho }$ is the density of the fluid,^[15]
• ${\displaystyle v}$ is the speed of the object relative to the fluid,
• ${\displaystyle A}$ is the cross sectional area, and
• ${\displaystyle C_{D}}$ is the drag coefficient – a dimensionless number.

The drag coefficient depends on the shape of the object and on the Reynolds number

where

• ${\displaystyle D}$ is some characteristic diameter or linear dimension. Actually, ${\displaystyle D}$ is the equivalent diameter ${\displaystyle D_{e}}$ of the object. For a sphere, ${\displaystyle D_{e}}$ is the D of the sphere itself.
• For a rectangular shape cross-section in the motion direction, ${\displaystyle D_{e}=1.30\cdot {\frac {(a\cdot b)^{0.625}}{(a+b)^{0.25}}}}$, where a and b are the rectangle edges.
• ${\displaystyle {\nu }}$ is the kinematic viscosity of the fluid (equal to the dynamic viscosity ${\displaystyle {\mu }}$ divided by the density ${\displaystyle {\rho }}$ ).

At low ${\displaystyle R_{e}}$, ${\displaystyle C_{D}}$ is asymptotically proportional to ${\displaystyle R_{e}^{-1}}$, which means that the drag is linearly proportional to the speed, i.e. the drag force on a small sphere moving through a viscous fluid is given by the Stokes Law:

At high ${\displaystyle R_{e}}$, ${\displaystyle C_{D}}$ is more or less constant and drag will vary as the square of the speed. The graph to the right shows how ${\displaystyle C_{D}}$ varies with ${\displaystyle R_{e}}$ for the case of a sphere. Since the power needed to overcome the drag force is the product of the force times speed, the power needed to overcome drag will vary as the square of the speed at low Reynolds numbers and as the cube of the speed at high numbers.

It can be demonstrated that drag force can be expressed as a function of a dimensionless number, which is dimensionally identical to the Bejan number.^[16] Consequently, drag force and drag coefficient can be a function of Bejan number. In fact, from the expression of drag force it has been obtained:

and consequently allows expressing the drag coefficient ${\displaystyle C_{D}}$ as a function of Bejan number and the ratio between wet area ${\displaystyle A_{w}}$ and front area ${\displaystyle A_{f}}$:^[16] where ${\displaystyle Re_{L}}$is the Reynolds number related to fluid path length L.

At high velocity

As mentioned, the drag equation with a constant drag coefficient gives the force experienced by an object moving through a fluid at relatively large velocity (i.e. high Reynolds number, Re > ~1000). This is also called quadratic drag. The equation is attributed to Lord Rayleigh, who originally used L² in place of A (L being some length).