Euler–Bernoulli beam theory (also known as engineer's beam theory or classical beam theory)^[1] is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case corresponding to small deflections of a beam that is subjected to lateral loads only. By ignoring the effects of shear deformation and rotatory inertia, it is thus a special case of Timoshenko–Ehrenfest beam theory. It was first enunciated circa 1750,^[2] but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution.

Additional mathematical models have been developed, such as plate theory, but the simplicity of beam theory makes it an important tool in the sciences, especially structural and mechanical engineering.

History

Prevailing consensus is that Galileo Galilei made the first attempts at developing a theory of beams, but recent studies argue that Leonardo da Vinci was the first to make the crucial observations. Da Vinci lacked Hooke's law and calculus to complete the theory, whereas Galileo was held back by an incorrect assumption he made.^[3]

The Bernoulli beam is named after Jacob Bernoulli, who made the significant discoveries. Leonhard Euler and Daniel Bernoulli were the first to put together a useful theory circa 1750.^[4]

Static beam equation

The Euler–Bernoulli equation describes the relationship between the beam's deflection and the applied load:^[5]

The curve ${\displaystyle w(x)}$ describes the deflection of the beam in the ${\displaystyle z}$ direction at some position ${\displaystyle x}$ (recall that the beam is modeled as a one-dimensional object). ${\displaystyle q}$ is a distributed load, in other words a force per unit length (analogous to pressure being a force per area); it may be a function of ${\displaystyle x}$, ${\displaystyle w}$, or other variables. ${\displaystyle E}$ is the elastic modulus and ${\displaystyle I}$ is the second moment of area of the beam's cross section. ${\displaystyle I}$ must be calculated with respect to the axis which is perpendicular to the applied loading.^{[N 1]} Explicitly, for a beam whose axis is oriented along ${\displaystyle x}$ with a loading along ${\displaystyle z}$, the beam's cross section is in the ${\displaystyle yz}$ plane, and the relevant second moment of area is

${\displaystyle I=\iint z^{2}\;dy\;dz,}$

where it is assumed that the centroid of the cross section occurs at ${\displaystyle y=z=0}$.

Often, the product ${\displaystyle EI}$ (known as the flexural rigidity) is a constant, so that

${\displaystyle EI{\frac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=q(x).\,}$

This equation, describing the deflection of a uniform, static beam, is used widely in engineering practice. Tabulated expressions for the deflection ${\displaystyle w}$ for common beam configurations can be found in engineering handbooks. For more complicated situations, the deflection can be determined by solving the Euler–Bernoulli equation using techniques such as "direct integration", "Macaulay's method", "moment area method, "conjugate beam method", "the principle of virtual work", "Castigliano's method", "flexibility method", "slope deflection method", "moment distribution method", or "direct stiffness method".

Sign conventions are defined here since different conventions can be found in the literature.^[5] In this article, a right-handed coordinate system is used with the ${\displaystyle x}$ axis to the right, the ${\displaystyle z}$ axis pointing upwards, and the ${\displaystyle y}$ axis pointing into the figure. The sign of the bending moment ${\displaystyle M}$ is taken as positive when the torque vector associated with the bending moment on the right hand side of the section is in the positive ${\displaystyle y}$ direction, that is, a positive value of ${\displaystyle M}$ produces compressive stress at the bottom surface. With this choice of bending moment sign convention, in order to have ${\displaystyle dM=Qdx}$, it is necessary that the shear force ${\displaystyle Q}$ acting on the right side of the section be positive in the ${\displaystyle z}$ direction so as to achieve static equilibrium of moments. If the loading intensity ${\displaystyle q}$ is taken positive in the positive ${\displaystyle z}$ direction, then ${\displaystyle dQ=-qdx}$ is necessary for force equilibrium.

Successive derivatives of the deflection ${\displaystyle w}$ have important physical meanings: ${\displaystyle dw/dx}$ is the slope of the beam, which is the anti-clockwise angle of rotation about the ${\displaystyle y}$-axis in the limit of small displacements;

${\displaystyle M=-EI{\frac {d^{2}w}{dx^{2}}}}$

is the bending moment in the beam; and

${\displaystyle Q=-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}$

is the shear force in the beam.

The stresses in a beam can be calculated from the above expressions after the deflection due to a given load has been determined.

Derivation of the bending equation

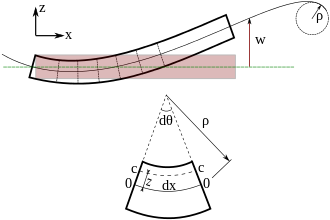
Because of the fundamental importance of the bending moment equation in engineering, we will provide a short derivation. We change to polar coordinates. The length of the neutral axis in the figure is ${\displaystyle \rho d\theta .}$ The length of a fiber with a radial distance ${\displaystyle z}$ below the neutral axis is $$Zdroj:https://en.wikipedia.org?pojem=Euler–Bernoulli_beam_theory
>Text je dostupný pod licencí Creative Commons Uveďte autora – Zachovejte licenci, případně za dalších podmínek. Podrobnosti naleznete na stránce Podmínky užití.