This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (February 2010) (Learn how and when to remove this template message)

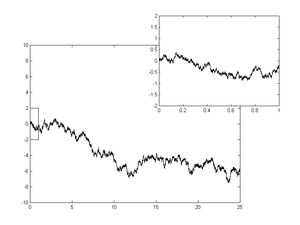
In mathematics, the Wiener process is a real-valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion.^[1] It is often also called Brownian motion due to its historical connection with the physical process of the same name originally observed by Scottish botanist Robert Brown. It is one of the best known Lévy processes (càdlàg stochastic processes with stationary independent increments) and occurs frequently in pure and applied mathematics, economics, quantitative finance, evolutionary biology, and physics.

The Wiener process plays an important role in both pure and applied mathematics. In pure mathematics, the Wiener process gave rise to the study of continuous time martingales. It is a key process in terms of which more complicated stochastic processes can be described. As such, it plays a vital role in stochastic calculus, diffusion processes and even potential theory. It is the driving process of Schramm–Loewner evolution. In applied mathematics, the Wiener process is used to represent the integral of a white noise Gaussian process, and so is useful as a model of noise in electronics engineering (see Brownian noise), instrument errors in filtering theory and disturbances in control theory.

The Wiener process has applications throughout the mathematical sciences. In physics it is used to study Brownian motion, the diffusion of minute particles suspended in fluid, and other types of diffusion via the Fokker–Planck and Langevin equations. It also forms the basis for the rigorous path integral formulation of quantum mechanics (by the Feynman–Kac formula, a solution to the Schrödinger equation can be represented in terms of the Wiener process) and the study of eternal inflation in physical cosmology. It is also prominent in the mathematical theory of finance, in particular the Black–Scholes option pricing model.

Characterisations of the Wiener process

The Wiener process ${\displaystyle W_{t}}$ is characterised by the following properties:^[2]

1. ${\displaystyle W_{0}=0}$ almost surely
2. ${\displaystyle W}$ has independent increments: for every ${\displaystyle t>0,}$ the future increments ${\displaystyle W_{t+u}-W_{t},}$ ${\displaystyle u\geq 0,}$ are independent of the past values ${\displaystyle W_{s}}$, ${\displaystyle s<t.}$
3. ${\displaystyle W}$ has Gaussian increments: ${\displaystyle W_{t+u}-W_{t}}$ is normally distributed with mean ${\displaystyle 0}$ and variance ${\displaystyle u}$, ${\displaystyle W_{t+u}-W_{t}\sim {\mathcal {N}}(0,u).}$
4. ${\displaystyle W}$ has almost surely continuous paths: ${\displaystyle W_{t}}$ is almost surely continuous in ${\displaystyle t}$.

That the process has independent increments means that if 0 ≤ s₁ < t₁ ≤ s₂ < t₂ then W_t1 − W_s1 and W_t2 − W_s2 are independent random variables, and the similar condition holds for n increments.

An alternative characterisation of the Wiener process is the so-called Lévy characterisation that says that the Wiener process is an almost surely continuous martingale with W₀ = 0 and quadratic variation = t (which means that W_t² − t is also a martingale).

A third characterisation is that the Wiener process has a spectral representation as a sine series whose coefficients are independent N(0, 1) random variables. This representation can be obtained using the Karhunen–Loève theorem.

Another characterisation of a Wiener process is the definite integral (from time zero to time t) of a zero mean, unit variance, delta correlated ("white") Gaussian process.^[3]

The Wiener process can be constructed as the scaling limit of a random walk, or other discrete-time stochastic processes with stationary independent increments. This is known as Donsker's theorem. Like the random walk, the Wiener process is recurrent in one or two dimensions (meaning that it returns almost surely to any fixed neighborhood of the origin infinitely often) whereas it is not recurrent in dimensions three and higher (where a multidimensional Wiener process is a process such that its coordinates are independent Wiener processes).^[4] Unlike the random walk, it is scale invariant, meaning that

is a Wiener process for any nonzero constant α. The Wiener measure is the probability law on the space of continuous functions g, with g(0) = 0, induced by the Wiener process. An integral based on Wiener measure may be called a Wiener integral.

Wiener process as a limit of random walk

Let ${\displaystyle \xi _{1},\xi _{2},\ldots }$ be i.i.d. random variables with mean 0 and variance 1. For each n, define a continuous time stochastic process

This is a random step function. Increments of ${\displaystyle W_{n}}$ are independent because the ${\displaystyle \xi _{k}}$ are independent. For large n, ${\displaystyle W_{n}(t)-W_{n}(s)}$ is close to ${\displaystyle N(0,t-s)}$ by the central limit theorem. Donsker's theorem asserts that as ${\displaystyle n\to \infty }$, ${\displaystyle W_{n}}$ approaches a Wiener process, which explains the ubiquity of Brownian motion.^[5]

Properties of a one-dimensional Wiener process

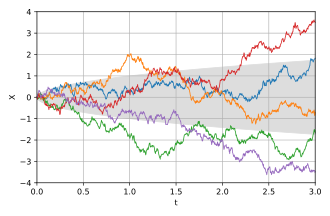
Basic properties

The unconditional probability density function follows a normal distribution with mean = 0 and variance = t, at a fixed time t: